LABORATORIO VIRTUAL DE MATEMÁTICAS
CONTENIDOS
Una ecuación de segundo grado es toda expresión de la forma:
ax2 + bx +c = 0 con a ≠ 0.
Se resuelve mediante la siguiente fórmula:
Si es a < 0, multiplicamos los dos miembros por (−1).
La solución es x = 0.
ax2 + bx = 0
Extraemos factor común x.
Igualamos cada factor a 0 y resolvemos las ecuaciones de 1er grado.
x = 0.
![]()
ax2 + c = 0
Despejamos:
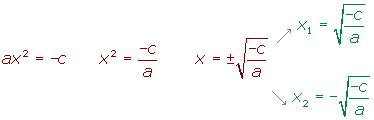
ax2 +bx +c = 0
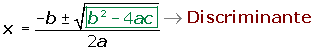
b2 − 4ac se llama discriminante de la ecuación y permite averiguar en cada ecuación el número de soluciones. Podemos distinguir tres casos:
b2 − 4ac > 0
La ecuación tiene dos soluciones, que son números reales distintos.
b2 − 4ac = 0
La ecuación tiene una solución doble.
b2 − 4ac < 0
La ecuación no tiene soluciones reales.
La suma de las soluciones de una ecuación de segundo grado es igual a:
![]()
El producto de las soluciones de una ecuación de segundo grado es igual a:
![]()
Si conocemos las raíces de una ecuación, podemos escribir ésta como:
![]()
Siendo S = x1 + x2 y P = x1 · x2
a x2 + bx +c = 0
a · (x -x1 ) · (x -x2 ) = 0
La ecuaciones racionales son ecuaciones en las que aparecen fracciones polinómicas.
Para resolverlas se multiplican ambos miembros de la ecuación por el mínimo común múltiplo de los denominadores.
Debemos comprobar las soluciones, para rechazar posibles soluciones extrañas provenientes de la ecuación transformada (la resultante de multiplicar por el mínimo común múltiplo), pero que no lo son de la ecuación original.
Son ecuaciones de cuarto grado sin términos de grado impar:
ax4 + bx2 + c = 0
Para resolverlas, efectuamos el cambio x2 = t, x4 = t2; con lo que genera una ecuación de segundo grado con la incógnita t:
at2 + bt + c = 0
Por cada valor positivo de t habrá dos valores de x:
![]()
Las ecuaciones irracionales son aquellas que tienen la incógnita bajo el signo radical.
Resolución:
1º Se aísla un radical en uno de los dos miembros, pasando al otro miembro el resto de los términos, aunque tengan también radicales.
2º Se elevan al cuadrado los dos miembros.
3º Se resuelve la ecuación obtenida.
4º Se comprueba si las soluciones obtenidas verifican la ecuación inicial. Hay que tener en cuenta que al elevar al cuadrado una ecuación se obtiene otra que tiene las mismas soluciones que la dada y, además las de la ecuación que se obtiene cambiando el signo de uno de los miembros de la ecuación.
5º Si la ecuación tiene varios radicales, se repiten las dos primeras fases del proceso hasta eliminarlos todos.
Es una ecuación de cualquier grado escrita de la forma P(x) = 0, el polinomio P(x) se puede descomponer en factores de primer y segundo grado, entonces basta igualar a cero cada uno de los factores y resolver las ecuaciones de primer grado y de segundo grado resultantes.
Utilizamos el teorema del resto y la regla de Ruffini.
Este método consiste en utilizar el método de reducción de manera que en cada ecuación tengamos una incógnita menos que en la ecuación precedente.
1º Ponemos como primera ecuación la que tenga el coeficiente en x más bajo.
2º Hacemos reducción con la 1ª y 2ª ecuación, para eliminar el término en x de la 2ª ecuación. Después ponemos como segunda ecuación el resultado de la operación:
E'2 = E2 − 3E1
3º Hacemos lo mismo con la ecuación 1ª y 3ª ecuación, para eliminar el término en x.
E'3 = E3 − 5E1
4º Tomamos las ecuaciones 2ª y 3ª, trasformadas, para hacer reducción y eliminar el término en y.
E''3 = E'3 − 2E'2
5º Obtenemos el sistema equivalente escalonado.
6º Encontrar las soluciones.
Un sistema de ecuaciones es no lineal, cuando al menos una de sus ecuaciones no es de primer grado.
La resolución de estos sistemas se suele hacer por el método de sustitución, para ello seguiremos los siguientes pasos:
1º Se despeja una incógnita en una de las ecuaciones, preferentemente en la de primer grado.
2º Se sustituye el valor de la incógnita despejada en la otra ecuación.
3º Se resuelve la ecuación resultante.
4º Cada uno de los valores obtenidos se sustituye en la otra ecuación, se obtienen así los valores correspondientes de la otra incógnita.


