LABORATORIO VIRTUAL DE MATEMÁTICAS
CONTENIDOS
Trabajar en álgebra consiste en manejar relaciones numéricas en las que una o más cantidades son desconocidas. Estas cantidades se llaman variables, incógnitas o indeterminadas y se representan por letras.
Una expresión algebraica es una combinación de letras y números ligada por los signos de las operaciones: adición, sustracción, multiplicación, división y potenciación.
El valor numérico de una expresión algebraica es el número que se obtiene al sustituir las letras de la misma por números determinados y efectuar las operaciones indicadas en la expresión.
Un monomio es una expresión algebraica en la que las únicas operaciones que aparecen entre las variables son el producto y la potencia de exponente natural.
El coeficiente del monomio es el número que aparece multiplicando a las variables.
La parte literal está constituida por las letras y sus exponentes.
El grado de un monomio es la suma de todos los exponentes de las letras o variables.
Dos monomios son semejantes cuando tienen la misma parte literal.
Suma de Monomios
Sólo podemos sumar monomios semejantes.
La suma de los monomios es otro monomio que tiene la misma parte literal y cuyo coeficiente es la suma de los coeficientes.
Producto de un número por un monomio
El producto de un número por un monomio es otro monomio semejante cuyo coeficiente es el producto del coeficiente de monomio por el número.
Producto de monomios
El producto de monomios es otro monomio que tiene por coeficiente el producto de los coeficientes y cuya parte literal se obtiene multiplicando las potencias que tenga la misma base.
Cociente de monomios
El cociente de monomios es otro monomio que tiene por coeficiente el cociente de los coeficientes y cuya parte literal se obtiene dividiendo las potencias que tenga la misma base.
Un polinomio es una expresión algebraica de la forma:
P(x) = an x n + an - 1 x n - 1 + an - 2 x n - 2 + ... + a1 x 1 + a 0
Siendo an, an - 1 ... a1 , ao números, llamados coeficientes.
n un número natural.
x la variable o indeterminada.
ao es el término independiente.
Grado de un polinomio
El grado de un polinomio P(x) es el mayor exponente al que se encuentra elevada la variable x.
Polinomio completo
Es aquel que tiene todos los términos desde el término independiente hasta el término de mayor grado
Polinomio ordenado
Un polinomio está ordenado si los monomios que lo forman están escritos de mayor a menor grado.
Polinomios iguales
Dos polinomios son iguales si verifican:
Los dos polinomios tienen el mismo grado.
Los coeficientes de los términos del mismo grado son iguales.
Valor numérico de un polinomio
Es el resultado que obtenemos al sustituir la variable x por un número cualquiera.
Suma de polinomios
Para sumar dos polinomios se suman los coeficientes de los términos del mismo grado.
La diferencia consiste en sumar el opuesto del sustraendo.
Multiplicación de polinomios
Producto de un número por un polinomio
Es otro polinomio que tiene de grado el mismo del polinomio y como coeficientes el producto de los coeficientes del polinomio por el número.
Producto de un monomio por un polinomio
Se multiplica el monomio por todos y cada uno de los monomios que forman el polinomio.
Producto de polinomio>
1 Se multiplica cada monomio del primer polinomio por todos los elementos segundo polinomio.
2 Se suman los monomios del mismo grado.
División de polinomios
P(x) : Q(x)
A la izquierda situamos el dividendo. Si el polinomio no es completo dejamos huecos en los lugares que correspondan.
A la derecha situamos el divisor dentro de una caja.
Dividimos el primer monomio del dividendo entre el primer monomio del divisor.
Multiplicamos cada término del polinomio divisor por el resultado anterior y lo restamos del polinomio dividendo:
Volvemos a dividir el primer monomio del dividendo entre el primer monomio del divisor. Y el resultado lo multiplicamos por el divisor y lo restamos al dividendo.
Repetimos el proceso anterior hasta que el grado del resto sea menor que el grado del divisor, y por tanto no se puede continuar dividiendo.
Para comprobar si la operación es correcta, utilizaríamos la prueba de la división:
D = d · c + r
Una fracción algebraica es el cociente de dos polinomios y se representa por:
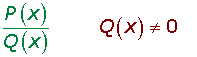
P(x) es el numerador y Q(x) el denominador.
Fracciones algebraicas equivalentes
Dos fracciones algebraicas
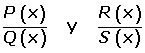
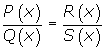
si se verifica que P(x) · S(x) = Q(x) · R(x).
Dada una fracción algebraica, si multiplicamos el numerador y el denominador de dicha fracción por un mismo polinomio distinto de cero, la fracción algebraica resultante es equivalente a la dada.
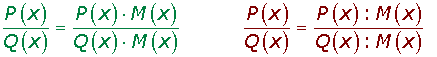
Para simplificar una fracción algebraica se divide el numerador y el denominador de la fracción por un polinomio que sea factor común de ambos.
Reducción de fracciones algebraicas a común denominador
Dadas dos fracciones algebraicas, reducirlas a común denominador es encontrar dos fracciones algebraicas equivalentes con el mismo denominador.
1Descomponemos los denominadores en factores para hallarles el mínimo común múltiplo, que será el común denominador.
2Dividimos el común denominador entre los denominadores de las fracciones dadas y el resultado lo multiplicamos por el numerador correspondiente.
Operaciones con fracciones algebraicas
Suma y diferencia de fracciones algebraicas
Fracciones algebraicas con igual denominador
La suma de fracciones algebraicas con el mismo denominador es otra fracción algebraica con el mismo denominador y cuyo numerador es la suma de los numeradores.
Fracciones algebraicas con distinto denominador
En primer lugar se ponen las fracciones algebraica a común denominador, posteriormente se suman los numeradores.
Producto de fracciones algebraicas
El producto de dos fracciones algebraicas es otra fracción algebraica donde el numerador es el producto de los numeradores y el denominador es el producto de los denominadores.
Cociente de fracciones algebraicas
El cociente de dos fracciones algebraicas es otra fracción algebraica con numerador el producto del numerador de la primera por el denominador de la segunda, y con denominador el producto del denominador de la primera por el numerador de la segunda.


