SISTEMA DE ECUACIONES

Dos ecuaciones con dos incógnitas forman un sistema, cuando lo que pretendemos de ellas es encontrar su solución común

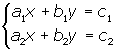
La solución de un sistema es un par de números x1, y1 , tales que reemplazando x por x1 e y por y1, se satisfacen a la vez ambas ecuaciones.

Sistemas equivalentes
Dos sistemas de ecuaciones son equivalentes cuando tienen la misma solución.

Criterios de equivalencia

1º Si a ambos miembros de una ecuación de un sistema se les suma o se les resta una misma expresión, el sistema resultante es equivalente.
2º Si multiplicamos o dividimos ambos miembros de las ecuaciones de un sistema por un número distinto de cero, el sistema resultante es equivalente.
3º Si sumamos o restamos a una ecuación de un sistema otra ecuación del mismo sistema, el sistema resultante es equivalente al dado.
4º Sin en un sistema se sustituye una ecuación por otra que resulte de sumar las dos ecuaciones del sistema previamente multiplicadas o divididas por números no nulos, resulta otro sistema equivalente al primero.
5º Si en un sistema se cambia el orden de las ecuaciones o el orden de las incógnitas, resulta otro sistema equivalente.

Resolución de sistemas de ecuaciones

Método de sustitución

1 Se despeja una incógnita en una de las ecuaciones.
2 Se sustituye la expresión de esta incógnita en la otra ecuación, obteniendo un ecuación con una sola incógnita.
3 Se resuelve la ecuación.
4 El valor obtenido se sustituye en la ecuación en la que aparecía la incógnita despejada.
5 Los dos valores obtenidos constituyen la solución del sistema.

Método de igualación

1 Se despeja la misma incógnita en ambas ecuaciones.
2 Se igualan las expresiones, con lo que obtenemos una ecuación con una incógnita.
3 Se resuelve la ecuación.
4 El valor obtenido se sustituye en cualquiera de las dos expresiones en las que aparecía despejada la otra incógnita.
5 Los dos valores obtenidos constituyen la solución del sistema.

Método de reducción

1 Se preparan las dos ecuaciones, multiplicándolas por los números que convenga.
2 La restamos, y desaparece una de las incógnitas.
3 Se resuelve la ecuación resultante.
4 El valor obtenido se sustituye en una de las ecuaciones iniciales y se resuelve.
5 Los dos valores obtenidos constituyen la solución del sistema.

Tipos de sistemas

Sistema compatible determinado
Tiene una sola solución.
Gráficamente la solución es el punto de corte de las dos rectas.
Sistema compatible indeterminado
El sistema tiene infinitas soluciones.
Gráficamente obtenemos dos rectas coincidentes. Cualquier punto de la recta es solución.
Sistema incompatible
No tiene solución
Gráficamente obtenemos dos rectas paralelas.